・PV図よりもとめるということがわからず、TV^(γ-1)=Cをファンデルワールスの式につっこんで挫折しました。１ｈを返して下さい。ただし他の熱力の授業をとったらもっと時間を取られたとおもうので、すでに１ｈ帰ってきている気がするためOKです。
うむ、ファンデルワールスは関係ないなぁ、笑。カルノーサイクルは理想気体をつかっているので。カルノーサイクルは授業をぼーときいてわかった気になっても、案外自分ではできないものなので、一度は自分で考えたり手を動かしたりする必要はあるかと思います。君の１ｈは決して無駄ではないのだ！
・熱機関の原理が液体→気体の体積変化から気体の膨張に変わったのは何故ですか？準静的でない過程は何故さかのぼれないのですか？
カルノーがサイクルを考察したときは、液体を含む状態方程式が詳しくわかっていなかったので、理想気体を使って簡単化をしたのだと思っています。つまりは計算できるから理想気体にした、という理解でいいと思います。最初にやった研究だからね。作業物質を一般の物質にしたらどうなるか、は次週の授業のメインの課題になります。準静的でない過程がさかのぼれないのは、今回の授業の最後にやった断熱過程についての不等式などでわかります。もどせないんですよ、普通は。また来週詳しくやりますね。
・わかりやすいです。
どうもどうも。
・僕は世界史の中でカエサルが一番好きなのですが、先生は誰がお気に入りですか？
漫画「ヒストリエ」が気になってまして、アレキサンダー大王ですかねぇ。
・大気圏突入のときになぜ燃えるかの話し、加藤先生のあと、他二人の先生が同じ話しをしていました。流行っているんですねww
Twitterでひところ話題になっていたからだと思われます。私が一番先でよかった。（というか、熱力学の授業でいうべき内容ですよね？？？）
・噛み砕いて説明してくださってありがたいです。
そろそろ新しい内容も増えてきます。頑張ってついてきてくださいね〜
・大学の必修授業で面白いと感じられているのは今のところ熱力・力学・ドイツ語くらいです。ありがとうございます。
力学もいい先生なんですね。よかったです。第二外国語は、私は本当にいやでいやで仕方なかったです・・・
・物理的考察は好きなのですが、それで出てきた式を数学的に変形していくのが苦手なので、大学の物理学が全体的にきつい、、、
数学は物理を堪能するためには必須の「言語」です。食わず嫌いせずに学んでください。理解したら、すごく感動しますよ。
・最大熱効率を求める際にlogが消えてしまうのは気持ちよい。こんなにきれいに表せるものなんだなあ、と感動に近い感覚を覚えた。短命だけど後世に名を残す人生と、凡人でありながら長生きする人生、個人的には前者を魅力的に思えてしまいました。
カルノーサイクルの効率、きれいですよね。ただ、私が学生のときに受けた授業では「そもそもなんでカルノーサイクルを考えるのだ？？？」というほうが気になって、あまり感動できなかった記憶があります。私の授業では、「なんでカルノーはこんなことを考えたのか」を自分なりに整理したので、素直に感動できたのかもしれませんね。よかったです。あと、私はやっぱり凡人でよいです、笑。
・1-T_L/T_H, W_qについては、”存在している”ということが効いているという理解であってますか？
そうですね。逆さに回せる唯一のサイクル（過程）が存在する、というのが効いていると思います。
・講義もノートもとても分かりやすく、速度も良い感じでとても助かります。
ノートはあとから見返してわかるように板書してます。ぜひノートを読み直して復習してください。
・各講ごとにテーマが一つ決まっていて、時間内にしっかり終わらせているので、復習がしやすくていい授業だと思いました。また、ネットやTwitterを駆使していて好感がもてた。
時間内に終わってないときもありますが、、、どんまい。Twitterは趣味です。この授業の感想＋返事も趣味です。
・SEGの授業受けているみたいで楽しいです。（物理受けてなかったけど。）
私は中学数学がメインで、高校物理はあんまり授業がうまくいった感じじゃないんですよね、苦笑。
・Twitterバズってて流れてきたのが一番印象的です（笑）
いやぁ、なんであんなさもないネタがバズるのか、不思議です。フォロワーの人とくだらないギャグ合戦をしているほうが、よっぽど頭を使ってます、笑。
・質問：問題１（３）でやり方が思いつかず、log p + log V = log T +log n + log Rという式からd(log p)+d(log V) = d(log T) を導出してしまいましたが、この式変形が正しいのかよくわかりません。間違っていれば、正しい方法を教えていただけると助かります。よろしくお願いします。
はい、これで大丈夫です。dT, dp, dVは考えなければいけませんが、n,Rは一定なのでdn, dRなどは考える必要がありません。いいかえると、d(log n) = dn/nとなるのですが、dn=0なのでこのような項は考えなくてもいい、ということになります。
第４講のポアソンの式の導出過程で、(p,V,T)→(p+dp,V+dV,T+dT)となったときの気体がされた仕事dWをdW=-pdVとしていますが、圧力も変化しているのでこれでよいのかひっかかりました。これは微小変化を考えているので、近似的にdW=-pdVとしているという解釈でよいのでしょうか。
pが変化することによる補正は、高次の微小量(dV dpを含む)になるので無視しています。dVが微小量だからできることで、これが有限の変化量だったら、ご指摘の通りpの変化の効果も考えないといけません。
・ニコニコのコメントのように黒板の上にスクリーンをつけてみんなの意見をリアルタイムで共有したい。（進度はちょうどいいと思います。）
最近そういうシステムもあるようです。最近はVR（バーチャル・リアリティ）もでてきましたので、VR授業をしてみたいです。そして、しゃべっている人に黒板消しを投げつけてみたい。リアルでやったら問題になるけど、VRなら問題ないよね。そして、見事あたったら、退場とか、笑。
・授業の難易度は難しくなく、理解しやすいです。蒸気機関のしくみが印象に残りました。カルノーサイクルではなぜ断熱過程を使うのかをずっと知らなかったのですが、分かってよかったです。眠れぬ夜のための問題が楽しいです。
カルノーサイクルの意義がうまくつたわったようでよかったです。眠れぬ夜の問題が面白いとはなかなかの通ですね。出題したかいがあります。これからも時々だしますね。
・もうすぐ誕生日です！６月１日です！カルノーと一緒です！熱力学でとっても重要なカルノーと一緒ということで当然熱力学で５０可がとれるようにがんばります！授業で世界史の話をしてくれるのが嬉しいです。
カルノーにあやかって、準静的に粛々と勉強してください（？）。産業革命と熱力学の関わりは、ほんと面白いよね。
・前回書き忘れてすいませんでした。自分は浪人して予備校に通っていたのですが、予備校の授業のような軽快な授業をする大学の先生はなかなかいらっしゃらない（自分が受けた中では）ので楽しくリラックスして授業を受けられています。ところで第１講か第２講で話されていた”仮面ライダービルド”ですが、本も面白いので是非ご覧になってください。第○話の○を数式で表したのが一瞬でてくるのも気に入っています。
あの数式を考えている人は慶應大学にいるのですが、実は先にTwitter上で知っていて、でも実名はわからず、慶應大学に議論しにいったとき「はじめまして」と挨拶したときに「あ、あのTwitterの人なんですね！いつもお世話になってます。」という意味不明の会話をしました。仮面ライダービルドは娘が夢中です。また見てみます。
・授業がわかりやすくて、聞いていて面白いです。
どうも。印象に残ったことを簡単にかいてくれると、なおうれしい。
・最近何をするのもつまらなくてとても憂鬱です。寝たきりの未来が見えます。授業関係ないですね、すいません。
ちょっと心配です。学生相談所にいくなど、なんらかの行動をしたほうがいいと思います。一人暮らしなんだったら、なおさら。
・カルノーサイクルが懐かしいです（再履なので）
カルノーサイクル新鮮です（初の熱力学の授業なので）。
・先生の小話、けっこう好きです。たくさんのネタをお持ちなんですね。
塾の講師時代からの蓄積があるので。でもすごい勢いで消費中なので、新作もつくらねば。
・月曜で一番最初の授業で普通なら憂うつなのに来たいと思う授業。（ただし３限目から憂うつ）休憩の間の小話がとても面白い。もっと話してください。
こういう感想は本当にうれしいです。授業を楽しんでくれているようでなにより。小話の量ははいまのぐらいがちょうどいいですよ、笑。
・基礎を丁寧に説明して頂いているので、よく理解ができています（今のところ）今度こそ単位を取るように努力します。
今度こそ単位取って下さい！
・自分は歴史が好きなので、蒸気機関の話はとても興味深かったです。またこんな話をしていただけるとうれしいです。
歴史の話はこれでおしまいです。ごめん。代わりに身近な現象とからめていろいろな話題を話せると思います。
・授業の進度は今の程度だと、授業中に理解できることが多いので丁度良く感じています。雑談が面白いので、それがもっと聞けるとうれしいです。なので、もう少し進度がはやくなっても良いかなと感じています。
今年度、はじめて熱力学の授業を担当しました。初回は手探りなので、進度はどうしても遅れがちです。すいませんが、若干の遅さは許容してください。というか、初めての授業なのに堂々と「何年の授業してたかのように」授業をするふてぶてしさが、私の持ち味です、笑。
・高校のときにやった物理と久々に会うことは嫌だなぁと思っていましたが（今のところは）楽しく授業を受けることができています。余談も楽しく聞いています。
物理ってやつは、人につらく当たるやつだけど、実はいいやつなんだ。バカなやつだけど、つきやってあげてくれ（青春群像風）。
・＃熱力学Aのツイートは加点対象ですか？
減点対象・・・というの嘘で、もちろん成績とは何ら関係ありません。もし関係があったら、教務から呼び出しくらいます、笑。
・こないだ、教えていただいた「参考書について」に載っていた富田博之氏の講義ノートはもうすでにダウンロードしていたので、載っていたことにびっくりしました。ちなみにグーグルで「バイバイン」と検索したら、「バイバイン　宇宙滅亡」とでてきます。今回の雑談は特に面白かったです。これからもよろしくお願いいたします。
バイバイン、有名なんですね。雑談は何がうけるかぜんぜんわかりません。毎回全力投球して、そしてそれでも、たまにコケます。今後共よろしくお願いします。
・僕は結構微分を苦手としているので、今回のレポートの問題１の（３）のような問題は考えこんでしまいました。微分の式を分数のように扱うという考え方はまだ慣れませんが、便宜上優れているとは思います。
微小量をそのまま微小なものとして扱う式変形は、始めのうちはなれないかと思います。（特に数学者はそういう表記を嫌いますよね。）もちろん、すべての計算を微小量抜きでやることもできるのですが、そうすると、偏微分の諸公式を覚えないといけません。微小量がなくなって気持ち悪さはなくなるのだけど、覚える公式がふえちゃうのです。一長一短ですね。まぁ、慣れて下さい。少なくとも私の熱力学の講義の中では。
加藤先生の授業は分かりやすく説明していただいていると思っています。（他の熱力学の先生の授業をとってないので比較できませんが）何より１０分の休憩時間が非常にありがたいです。このままこの形式の授業を進められて下さい。
休み時間は重要だよね。人間の集中力は１時間が限度だと思うのです。
・生徒をおいてきぼりにしないその姿勢は、他の先生も見習ってほしいですね。毎回出席してます！
どうもどうも。授業中になるべく理解してもらおうと思っています。自分で手で動かしてみて考える機会として、レポートを課してますので、こちらも頑張ってやってくださいね。
・先生の説明が上手いので大して苦労することもなく理解できます。どうせなら力学も担当していただきたいです。
柏から通うのが大変です、苦笑。教育への貢献が業績として認められるといいのですが、評価が難しいんですよね。
・僕は他クラです。先生の授業を受けていると非常に分かりやすくて、生徒のことを考えてくれていて...泣きそうです。いかに去年が...数学も神の先生を他クラしていますが（笑）教員ガチャの影響って大きすぎるような...特に数学なんて一年間先生同じだし...（去年ガチャをはずしまくった二年生より）
先生によって本当に違いますからね。お気の毒ですが、頑張って生きてください。私の学生時代も似たようなものでした。「私だったらこうやって説明するのに」と怒っていたのをよく覚えています。大学の先生があとすこしだけ教育に熱心になるといいのにね。でも、いい歳になってわかりましたが、大学には授業は下手でも研究で尊敬できる人はたくさんいます。「教育できないひとをやめさせろ」というのはいいすぎです。なにごともバランス。
・数学力が試されて辛いです。毎回復習があるのがうれしいです。
数学はその都度、補足説明しますので、なんとかついてきてください。
・数学的な部分（偏微分や全微分、関数の記法等）を丁寧に教えてくださったことがとてもありがたかったです。
熱力学はその数学的なところでおいてけぼりになってしまうことが多いので、最初にまとめてみました。
・教科書は担当の先生のものを使う方が個人的には好きな事が多いです。というのも、字の使い方や教える順番が同じである場合が多いからです。
よくわかります。でも一方で、人間は怠惰な生き物なので、「試験前に教科書読んどけばいいや」となって、結局読まずに試験にいどむ、ということにもなりかねないので、ほどほどがいいかなぁと思います。
・(1)最近、大学の授業は習得すると非常に役に立つものばかりですが、習得するのに時間がかかるものが多いという印象を受けます。医・薬学部以外も６年制にしてほしいくらいです。
６年制にしたら親が泣く。
(2)LaTeXで板書をまとめるのにはまっているのですが、普通に見返した方が効率よく復習できる気がします。控えた方がいいんでしょうか？
TeXは学んでおいて損はないし、タイピングが速くなるようであればよいかと。あとは好みの問題です。
(3)高校までと違って試験で単位落とすかもしれないのがめちゃくちゃ怖いです。
そういうふうに恐怖感をもっている人のほうが、案外、単位を落とさないです。単位落とす人はそもそも授業にこないですよね・・・
(4)先生は授業を受けている学生のTwitterアカウントを特定していますか？
全部じゃないけど、一部は。授業関連のことをつぶやくと割りとすぐに発見されますよ。
・雑談も面白く、講義もわかりやすいので、毎回、楽しみにしています。途中の休みが本当にありがたいです。唯一の眠くならない授業です。
他の駒場の先生、頑張れ〜
・はじめ、問題１（３）をp,V,Tをtの関数として(2)の式を導出しようとしたが、そうしなくても上のように解くことができた。というか、（２）でも時間ｔの姿は全く見当たらない。状態方程式は時間発展を記述するのにとても有用なのに、ｔが全くでてこないから違和感がある。間違った感覚でしょうか。このような例は実は他にも存在するのでしょうか。
まず熱力学では通常は時間の概念があまりありません。時間発展との相性はあまりよくないのです。大学の入試問題で時々、運動方程式と組み合わせる問題がでますが、そこでは気体は常に熱平衡状態であることを仮定する必要があります。つまりピストンが動くような場合でも、準静的過程のみを考えています。しかし、一般にはピストンが動けば準静的ではないような変化が生じます（例えばピストンはしばらくすると止まってしまう）。準静的変化でないと、気体は熱平衡状態になっていないので、状態方程式が成り立ちません。ですので、状態方程式と時間発展との相性は最悪といえるでしょう。一方、ｔを本当の時刻と見ずに、パラメータとみなすのであれば、とても有益です。つまり、ｔを準静的過程を記述する媒介変数とみるのです。こうしてみると、(p,V,T)の変化は、(p(t), V(t), T(t))のような媒介変数表示による記述と見直すことができます。もし、dp, dT, dVなどの微小量が気持ち悪いのであれば、dtで割ってみてください。dp/dt, dT/dt, dV/dtなどがでてきますが、これは媒介変数ｔの導関数と考えることが可能です。微小量が苦手な人は、このように媒介変数表示ｔで表示して、dtでわり、微小量どうしの分数は導関数なんだと解釈すれば、少しはわかりやすくなるかと思います。（実際、数学者は常にそのように考えます。）
・（３）で何も気にせず微分してしまったのですが、これは「何で」微分しているんですか？高校数学で微分する際に「何で」微分するのかに気をつけろ！と言われてきたので少し違和感を感じています。熱力学なのであまり気にしないほうがよいのでしょうか？
ちょうど上記の答えがこの質問の答えになっているかと思います。いかがでしょうか。
・(1)情報熱力学に少し興味があります。この学問が意味するところは「観測結果に応じた操作を加えることで自然な状態より多くの仕事を取り出すことができ、その余分量は観測結果の情報量から求められる」ということでしょうか。
はい、そのとおりです。
W ≦-ΔF + k_B T I は何を根拠に求められたのでしょうか。（実験事実？）
いえいえ、この式は最近になって、ちゃんと証明されたものです。証明されたものなので、すごく価値があるんですよ。
(2)先生はニコニコ動画を見ていたらしいですが、どんな動画を見ていた（あるいは見ている）ので しょうか。
東方とか、MMDとかでしょうか。でも基本、なんでも見ましたよ。
(3)サメ映画とハルマゲドンシリーズをオススメします。（あと実写版デビルマン）
シャークネードでしょうか、メガ・シャークVSメカ・シャークでしょうか、笑。アルマゲドンは始めのやつしか見てない。チェックしてみます。実写版デビルマンは却下。
・熱力学は受験の時は捨てていた単元で、決して好きな単元ではないのですが、大学の座学の講義の中で唯一の眠くなりにくい授業だと思っているので、今では全然嫌いじゃないです。また、板書がおいつかなそうなタイミングで雑談をはさんでもらえることが多くて、とても助かってます。
熱力学が嫌いじゃなくなってよかったです。好きになる所までいってくれるとうれしいです。
・近いうちにTwitterでお会いする（かもしれません。）またおもしろい講義を期待しています。
Twitterは完全にお遊びなので、ゆる〜くやってます。
・雑談の一つとして、先生の研究内容や研究室のこと（障りのない範囲で）お教えいただければとてもうれしいです。ガンダムのお話もよろしくお願いします。
はい、いつか機会を見つけて、余談の中で話したいと思います。ガンダムネタはさすがにマニアックすぎるので自重します、笑。
・引き込まれる、分かりやすい講義。他の（特に数学の）教員などは加藤先生の講義を少しは見倣ったほうがよい。
「引き込まれる」という感想は、うれしいですね。やっと教師から噺家へとステップアップしたような感じ（嘘）。
・加藤先生の雑談はいつも聞いていておもしろいです。熱力学の講義はいまいち新しいことをやっている感じがしないのですが、気のせいでしょうか。
はい、今のところはそれほど新しくないです。しかし、来週からそろそろ熱力学の本領発揮で、新しいことが増えてきますよ。
・授業がわかりやすいので感謝しかない。（良い意味で）予備校の授業みたいだと思った。
頑張ってついてきてください〜
・朝永先生の「じわじわ」がとても気に入りました。彼の著作でお好きなものはありますか？読んでみたいです。ちなみに私も柏市民です。震災の年は地価こそ下がりましたが人口は増えたんだったような・・・先生のおかげでしょうかね。
「じわじわ」いいですよね。朝永先生の著作はどれもいいですが、「物理学とは何だろうか上・下」(岩波新書) とか「量子力学と私」(岩波文庫)が私は好きです。前者は啓蒙書、後者はエッセーです。私は流山市民ですが、流山も人口増えたと思います。柏も流山も、子供が増えつつ有って、活気がありますよね。残留放射能も問題ないレベルになりましたし、ほっとしています。
・授業めちゃ面白いです。ありがとうございます。再履修がんばります。
どうもどうも。頑張って出席してください。
・とても分かりやすいです。休憩時間の話、いつも待ち遠しいです。
ああ、だんだんハードルが上がっていく、笑。
・カルノーサイクルがこういうサイクルの中で最も効率的なことは、下の図でT_HとT_Lが決まっているときに（長方形をなすときにQ_L/Q_Hが明らかに最小）だからでいいですかね。カルノーの原理の説明的にカルノーより効率悪いやつの逆があると、第二法則に矛盾するっぽいんですが、効率悪い奴は逆に しようとすると、第二法則にひっかかるんですかね？(下の図は加藤が書き出したもの）

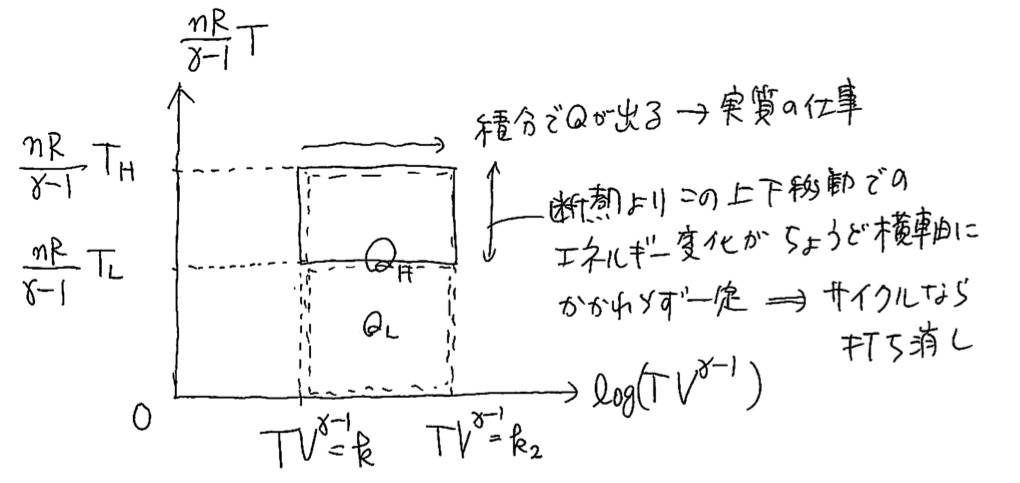
図の意味がちゃんとはわからなかったのですが、私が次の週に説明する内容に非常に近いですね。たぶんいいたいことは概ねあっていますが、細かいところをちゃんとつめる必要がある、ように見えます。ちなみに、横軸はとある有名な物理量（に定数をかけたもの）になってますね。どんな物理量かは、次週話すので、お楽しみに！