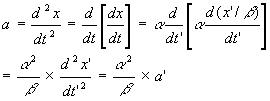
第六章. サイズと時間 ---力学相似を通して----
いよいよ夏も本番になりました。夏休みは誰にとっても、とても素敵な思いでの残る素敵な時間です。我々の体は夏になるととても活動的になります。我々の体は、夏にもっとも能力を発揮できるように仕組まれているのでしょう。しかし、夏休みはあっという間に過ぎてしまって、気がつけばもう学校にいかねばならなくなります。どうして、とても楽しい時間は、あっという間に過ぎてしまうのでしょう。そして、どうしてつらく悲しい時には、時間はとてもゆっくりと流れるのでしょう、、、
今回は、その「時間の流れる速さ」について、物理的に考えてみます。
映画の撮影で巨大な物(怪獣とか大きな岩など)を撮影する時に、撮影したいものを縮小した模型を使うことがあります。しかし何も考えずに撮影すると、見ている人に模型であることがばれてしまいます。皆さんも昔の映画を見ていて、明らかに模型だと分かるときが、ありますよね。では、何故模型だとばれるのかを考えてみましょう。
大きな岩が崖に上から落下する場合を考えて見ましょう。本物の岩であった場合は、落下時間 t [秒]と落下距離 h [m] の間には、
h = 4.9 t^2
という関係があります。これを縮小した模型を使って、同じように落下させたとしましょう。落下時間 t' と落下距離 h' の間には、やはり
h' = 4.9 t'^2
という関係があります。これらの2式の辺々を割り算すると、
h'/h = (t'/t)^2 ... (1)
という式が得られます。さてここで、この式の意味を考えて見ましょう。今、縮小模型を使っているので、h'<h です。すると当然落下するのにかかる時間は少なくて済みます(t'<t)。例えば、本来10秒かかって落ちるものが、5秒で落ちきってしまうというようなことになります。ですから、このまま縮小模型で撮影して本物の岩のように見せかけようとしてしまうと、物体は「異常に速く落ちるように見えます。すると見る人は「これはおもちゃだ」と感じてしまうわけです。
では、本物のように見せかけるには、どのようにしたらよいでしょうか?答えはかんたんです。撮影したフィルムをゆっくりと回せばいい!具体的には、時間を t/t' (>1)倍だけフィルムをゆっくり回すことにすればよいのです。例えば本当は10秒かかって落ちるものが、模型では5秒しかからないのであったら、撮影したフィルムを2倍だけゆっくりと回せばよいことになります。式(1)は、模型の縮小率 h'/h とかかる時間の比 t'/t の関係式を与えていますから、模型の縮小率が分かれば、どれぐらいゆっくりフィルムを回せばよいかも、すぐに計算できます。
ここまでは、撮影方法に関する説明でしたが、もっと想像力を働かせると面白い考え方に行き着きます。それは、「サイズの大きい物体では、時間の流れ方がゆっくりになるのではないか?」ということです。これは、ゾウがのっしのっしと歩くのと、ネズミがちょろちょろと走り回る様子を比べてみてもわかりますよね。生物に関する話題は後回しにして、もうしばらく物理の範囲内で、このことを調べて見ましょう。
前の節で、物体の自由落下に関して式(1)を導きましたが、別の方法で式(1)を導きびくこともできます。まずは運動方程式を考えましょう。鉛直下向きを x 軸正の向きとして、
ma = mg
となります。 m は物体の質量、a は加速度、g は重力加速度です。さてここで、考えている対象のサイズを β倍することを考えましょう。β倍した後の物体の座標を x' とすると、
x' = βx
となります。β<1 の時が縮小模型に対応します。ところで先ほども述べたように、サイズをかえると時間の流れる速さも異なってくると考えられるので、
t' = α t
として、時刻の進み方が α倍になったとします。これらの式を運動方程式に代入してみましょう。x=x'/β, t=t'/α と解き直して加速度 a に代入すると、
となります。よって、運動方程式は、
ma'×(α^2/β) = mg ... (2)
となります。
さて、ここが考えどころです。サイズをβ倍しているので、物体の運動の様子は異なったものになります。先ほどの特殊撮影の例でいえば、本来10秒かかって落下するものが、5秒で落ちてしまう、といったことです。しかし、時間の進め方まで変えると(つまりフィルムをゆっくり回すと)、縮小模型で撮影したものは、「本物の運動と区別できなく」なります。この「区別できない」というところがみそです。
これを式の上で示すにはどうすればよいでしょうか。これがとてもシンプルなのです。新しい座標と時刻 x', t' に対して、元の運動方程式と同じ形の式、
ma' = mg
が成り立てばよい!すると、元の x, t で表される運動と、サイズを変えた後の運動が、区別できなくなります。この方程式が成り立つためには、式(2)において、
α^2/β= 1
が成り立てば良いことがわかります。この式は、α = t'/t, β= x'/x を使って、
x'/x = (t'/t)^2
と変形できます。x=h, x'=h'とおけば、これは前の節で求めた式(1)とまったく一致します。
このようにサイズを変えるとともに、時間の進め方を変えると、元の運動と区別がつかなくなることを、「力学相似」といいます。相似というと、中学の幾何の証明を思い浮かべますよね。サイズを変えるというところは似ていますが、「力学相似」ではサイズの他に、時間がからんでくるところが異なります。
もう一つ面白い問題として、万有引力による惑星の運行を考えてみましょう。太陽の回りをまわる質量 m の惑星の運動方程式は、
ma = GMm/r^2
で与えられます。ここで、a は加速度の動径方向の成分、G は重力定数、r は太陽と惑星の間の距離です。先ほどと同じようにサイズと時刻の進み方を変えてみます。x'=βx, t'=αt として、運動方程式を書き直すと、先ほどと同じようにして、
ma'×(α^2/β) = GMm/r'^2 ×β^2 ... (3)
という式を得ます。ここでサイズをβ倍したので、太陽との距離もr'=βr としてβ倍しておきます。惑星の軌道の大きさが変われば、運動も異なってきますが、時間の進む速さをうまく調節すると、元の運動と区別できなくなります。この時は、x', t' についても、同じ運動方程式、
ma' = GMm/r'^2
が成り立つはずです。この式が成り立つためには、式(3)において、
α^2/β = β^2
が成り立たないといけないことがわかります。これを整理して、
β^3 = α^2 ... (4)
を得ます。さて、惑星は楕円運動していることがわかっていますので、この長半径を R としましょう。また、惑星が一周するのにかかる時間(周期)を T とします。さらにサイズを変えた時の惑星軌道の長軸半径を R'、周期を T' とします。サイズはβ倍、時間はα倍されているので、β = R'/R, およびα = T'/Tが成り立ちます。これらを式(4)に代入すると、
(R'/R)^3 = (T'/T)^2
を得ます。これより、長軸半径の3乗は周期の2倍に比例することがわかりました。この法則を我々は「ケプラーの第3法則」と呼んでいます。この法則を導くのに全く複雑な計算をしていないことに注意して下さい。「力学相似」を万有引力に適用しただけで、出てくるのです。
次に、生物におけるサイズと時間の関係についてお話ししましょう。生物を支配している時間というと、代表的なものとして「寿命」が挙げられます。ある動物の寿命を T としましょう。この動物のサイズと寿命との関係を考えたいのですが、サイズとして何を計れば良いのか曖昧です。そこで、体重 W に注目しましょう。動物の体の密度は動物によってそれほど変わらないので、体重がわかると動物の占めている体積がわかります。だから、W が動物のサイズを決めているとして良いでしょう。体重ならば、どんな動物でも簡単に計れます。
さて、いろいろな種類の恒温動物について、寿命と体重を調べていくうちに、二つの異なる種類の動物の寿命を T, T'、体重を W, W' とした時に、
(T'/T) = (W'/W)^(1/4)
がよく成り立っていることがわかってきました。もう少し分かりやすくするためにさらに、動物の体の体積と同じ体積の立方体の1辺の長さを L として、この L が動物のサイズ(長さ)を与えるとしましょう。この時、W=aL^3 が成り立ちます。ここで a は動物の体の密度で、動物の種類によってほぼ一定であることがわかるので、別の動物についても W'=aL'^3 ともかくことができます。これらを代入すると、
(T'/T) = (L'/L)^(3/4)
ともかけます。これが、生物におけるサイズと時間の関係を与えています。驚くべきことに、これは恒温動物に限らず、変温動物、微生物を含むあらゆる生物に対して成り立つ式になっていることもわかってきました。(ただし、恒温動物とは恒温動物と、変温動物とは変温動物と、微生物とは微生物と、という風に比べなくてはいけません。)
この式は、いままで述べてきた物理における力学相似ととても良く似ています。なぜこのような関係式が成り立つのか、とても知りたいところなのですが、未だにその理由はわかっていません。全く未知です。しかし、非常に多くの動物についてこの式が成り立っているので、これは偶然とは思えません。何か必ず生物特有のメカニズムがあるはずなのですが、、、
いままで見てきたように、物体のサイズと時間の間には、深い関係があることが分かっています。これは力学に限らず、生物に対しても成り立つことを解説してきました。時間の流れ方は、物体の大きさによっています。そして、おそらくゾウの感じている時間の流れは、ネズミの感じている時間の流れより、とてもゆっくりしていると推測できます。我々は、「時間の流れ方は、どんな生物も同じである」と考える傾向がありますが、それは誤りなのでしょう。
著者はさらに話しを進めて、「時間の流れる速さ」は人間の置かれている環境、個人の感情、時代によっても変わるものであると考えています。それは個人のライフスライルと深く関係していると思われます。例えば, 高校生の中だけでも, あくせくと勉強する人、ぼーとしてる人、恋愛に胸焦がす人、どっしりしていて落ち着いている人、本当に様々です。それらすべての人に対して、時間が同じ速さで流れていると言えるでしょうか?
最後に、このような問題が生じる根本的な原因は、我々の時間把握能力の未熟さにあることだけ指摘しておきます。皆さんは、どのように感じられるでしょうか?
この解説を書くに当たって、ランダウ-リフシッツ著「力学」(東京図書)および本川達雄著「ゾウの時間ネズミの時間」(中公新書)を参考にしました。特に後者は生物におけるサイズと時間の関係について詳細にわかりやすく述べられていますので、一読をお勧めします。