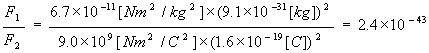
第四章. 物理学における単位
20xx年、人類はついに地球外知的生物とのコンタクトに成功した。超光速通信を駆使し、数年をかけてようやくお互いの言語を理解し合うようになったある日。
宇宙人「我々は、あなた達の素晴らしい文化をいろいろと聞いてきました。全くもって素晴らしい。今度是非我々のところにいらして下さい。ところで、あなた達のために特別に椅子やベッドを用意しなくてはいけません。そのために一つ聞いておきたいことがあります。あなた達の体の大きさは、一体どれくらいあるのでしょうか。」
我々「1.5から2メートルぐらいです。」
宇宙人「なるほど、なるほど。ところで1メートルってなんですか?」
我々「、、、」
我々は長さを測る時に単位としてメートルを使います。しかし、1メートルという長さは、単に「これが1メートル」と人間が勝手に決めただけのものです。宇宙人には、その基準となる長さがわからないので、「1.5メートル」とか言ってもわからないわけです。何も大きさを測るのにメートルを使う必要はありません。お互いが理解し合える基準となる長ささえあれば良いのです。例えば、先ほどの会話の続き
「、、、自然界にある最も軽い元素を持ってきて下さい。それを我々は水素と呼んでいます。水素原子の大きさは測れますよね?我々の大きさは、その水素原子の大きさの150億から200億倍位の大きさで、、、」
などと。宇宙人の住んでいる場所にも間違いなく水素原子は存在し、その大きさは地球上にあるものと変わらないはずですから、水素原子の大きさを長さの基準にとれば、お互いに理解し合えるのです。
我々は、物体の大きさを始めとして、物体のさまざまな性質(速度、位置、密度、温度、電気抵抗、などなど)の情報を他人に伝えるために、それらの性質を数値化します。その際に、何を基準にして測ったかを明らかにしなければいけません。それが「単位」です。物理では、必ずこれらの「数値化された」量の変化に注目します。例えば力学では物体の位置に注目しますし、熱学では物体の温度に注目します。
物体の性質を数値にする時には、何を基準にして測るか、つまり「単位」をどのようにとるかを、常に明記しなくてはなりません。(試験で単位を忘れて減点された経験は誰にでもあるでしょう。)「単位」を正しく理解することは、物理を学ぶ上でとても大切なことであります。今回は、この「単位」に焦点を当てて、お話することにしましょう。
物理で使われる基本的な量は、長さと質量、それに時間です。物理ではこれらの量を表すのに、それぞれ[m], [kg], [s](秒)を使います。このような単位のとり方を「MKS単位系」あるいは「SI単位系」と呼んでいます。(電磁気学にいくと、これらに加えて電荷の単位[C](クーロン)が加わります。)
単位に関する規則をまとめることにしましょう。まず、一つ目。
規則1: 単位の違う量を足したり引いたりしてはいけない。
例えば、「2 m」と「3 kg」を足したり引いたりすることはできません。高校生の物理の試験の解答を見ていると、この規則を破るような解答によくでくわします。例えば、
F = mg + v
といった解答はすぐに誤りであることがわかります。何故なら、mg は力の単位を持つのに対して、v は速度の単位を持つので、単位の違う量を足し合わせることになるからです。
規則2:単位の違う量を掛けたり割ったりすることはできる。
例えば、物体が3[s]の間に6[m]進んでいれば、物体の速度は、6[m]/3[s]=2[m/s]と計算できます。単位の違う量を掛けたり割ったりしてできた新しいの物理量は、新しい単位を持ちますが、それらは元の単位を掛け合わせたり割ったりすれば得られます。例えば、加速度a=dv/dt の単位は、[m/s]/[s] = [m/s^2]となります。(ここで1[m/s^2]とは、1[s]あたりに1[m/s]づつ速度が変化する時の加速度です。)
このようなことを繰り返すことによって、すべての物理量の単位をm, kg, s だけで表すことができます。例えば、MKS単位系で力の単位は[N](ニュートン)です。これは1[kg]の物体を1[m/s^2]の加速度で加速させるのに必要な力の大きさで、F=ma より、
1[N] = 1 [kg]×1[m/s^2]= 1 [kg m/s^2]
のように、kg, m, sを用いて表せます。同様にして、仕事の単位が1[J](ジュール)=1[kg m^2/s^2]、仕事率の単位が1[W](ワット)=1[kg m^2/s^3]であることも確かめられます。物理では混乱がないように、必ずこのようなMKS(SI)単位系を用いて計算を行なうようにしています。
規則3: 等式の両辺には、同じ単位の量がくる。
これは規則1と同じなのですが、新たに書きました。この規則を破るような解答が何と多いことか。例えば、力の大きさを求めたときに、
F=mg^2/(M+m)
とでてきたとします。(g は重力加速度)しかし、これは単位を考えると明らかに間違いですよね。右辺の単位は[m^2/s^4] となってしまって、左辺の単位と一致しません。このような単位の確認は比較的簡単に行えますし、これによって多くの計算ミスを防げます。ですから、物理の計算をするときには、常に単位のことを心に留めておいてください。
他にも、「振り子の周期って、T=2π√(L/g)だっけ、T=2π√(g/L)だっけ?」というような時も単位のことを考えれば、前者が正しいことはすぐにわかりますし、波の基本式、fλ=v (ここでf は振動数[1/s],λは波長[m], v は波の速さ[m/s])もすぐに導けるはずです。
この世には、単位の無い量(以下、無次元量と呼ぶことにします)も存在します。例えば、角度を測る時[rad](ラジアン)という単位を用いますが、これば便宜上そう呼ぶだけで実際には物理的な単位はありません。(理由は、円周角θと半径r, 孤長Lの関係式L=rθから明らかです。)よって円運動のところで出てくる角速度ω(単位時間当たりに回転する角度)の単位は、[1/s]となります。
その他には、はねかえり係数e や、静止摩擦係数μ,動摩擦係数μ’なども単位のない量です。これらの量は物質の材質や接触面の状態によって決まる定数です。
それから、こんな無次元量もあります。電荷-e, 質量m の2個の電子を距離r だけ離して固定します。この時に電子に働く万有引力の大きさF_1 は、
F_1 = Gm^2/r^2
と計算できます(G は重力定数)。一方、電子に働くクーロン反発力F_2は、
F_2 = ke^2/r^2
となります(k はクーロン定数)。この重力F_1 と電気力F_2の大きさの比をとってみましょう。するとr は消えてしまい、F_1/F_2 = Gm^2/ke^2 となります。ここに現れるすべての文字は定数ですから、実験で求められている値を代入してやって、
となります。ここで出てきた結果には、単位がありません。電子は自然界で最も基本的な粒子ですから、この数値は、自然界における重力の大きさと電気力の大きさの比を表したものだと考えられます。ここで、この数値がとてつもなく小さいことに注意して下さい。実は重力は、とってもとっても弱い力なのです。何故、重力がこれほどまでに小さいかは、今のところ誰にも説明できません。
(補足)でもこのおかげで、原子レベルでいろいろな計算をする時は、重力の影響を無視できます。しかし、物体が大きくなってくると質量は大きくなっていくのに対して、電荷はプラスとマイナスが打ち消しあって全体的にほぼ0になりますから、重力の方か大きくなります。
ところで、無次元の量には特別な性質があります。それは、「どんな単位系を使って計算しても、全く同じ値である」と言うことです。例えば我々がMKS単位系を使っても、宇宙人がXYZ単位系を使おうが、日本古来の尺貫法を使おうが、はねかえり係数を始めとする無単位量の値は同じになります。先ほど計算した、F_1/F_2という量は、どんな単位を用いても同じ値となるという意味で、普遍的な自然界の定数になっています。例えば、宇宙に向かって、2.4×10^(-43)という数値を電波で宇宙に向かって送信したとしますと、宇宙人はそれが何であるかしばらく試行錯誤したあとに、重力と電気力の比であることに気付くはずです。これが、単位のついている量だとうまくいきません。例えば、電子の質量9.1×10^(-31)[kg] を宇宙に送ってもだめです。宇宙人は、[kg]以外の単位を使っているのですから。
単位を考えることによって、とても役にたつ法則が得られることがあります。これからその1つの例をお目にかけましょう。
大きさのある物体を速さv の風の中に置くと、物体は空気から抵抗力を受けます。(台風の日に出歩くことを考えて見てください。)その抵抗力の大きさF は、風の強さがそれほど大きくなければ、風の速度v に比例することが知られていて、F=kv と表わすことができます。ここでk は物体の形状や空気の粘性によって決まる比例定数です。物体が半径a の球のとき、比例定数k は、次のように与えられます(ストークスの抵抗法則)。
k=6πaμ
ここでμは、空気の粘性率と呼ばれる量です。比例定数k は、物体の半径a に比例していることに注意してください。(直観的には、物体の断面積πa^2 に比例しそうなものですが、違います。また、前についている6πは便宜的なものだと考えてください。)
空気の粘性率μはどんな単位を持っているかを調べてみましょう。今までに挙げた2つの式から、μ=F/6πav と計算できますから、μの単位は、
[N]/[m][m/s]=[kg m/s^2]/[m^2/s]=[kg/(m・s)]
となります。さてここで、風のなかに物体を置いたとき、物体の回りを流れている空気の動きを考えてみましょう。空気の粘性率μや風の速さv、そして物体の大きさa などを変化させていくと、周りの空気の流れの様子も当然ながら変化していくと考えられます。あともう一つ、空気の密度ρ(単位は[kg/m^3] )によっても、空気の流れの様子が変わることがわかっています。この4つの量、μ,ρ,a,v から、単位のない無次元量を作ってみましょう。すると、
R = ρ a v/μ
という無次元量が作れることがわかります。(実際に単位がないことを確かめてみてください。)この量R のことをレイノルズ数といいます。
図1.半径aの円柱まわりの流体(水,空気など)の様子。Rはレイノルズ数。
実は、物体の周りの空気の流れは、このレイノルズ数だけで決まってしまうことがわかります。R が小さいうちは、周りの空気は静かに流れて乱れはありません(図1.(a))。しかし、R が大きくなるにつれて周りの空気の様子がどんどん変わってきます。まず、物体の後ろに対になった渦ができ始め(図1.(b))、さらにR が大きくなると渦が離れて、カルマン渦列と呼ばれる構造ができ始めます(図1.(c))。(ちなみに、このカルマン渦列は、コーヒーに浮いたミルクを匙でかき回してやれば、簡単に見ることができます。)さらにR が増えると物体の後方は乱流と呼ばれる乱れた状態になります(図1.(d))。物体の大きさa や風の速さv の大きさがどのように変化しても、R の値が同じであれば、周りの空気の流れの様子は同じになります。これをレイノルズの相似定理と呼びます。この法則の最大のポイントは、R が無次元量であることです。もし、R が単位を持つ量であれば、R の値は、単位系の取り方によっていくらでも違った値を取ってしまいますから、レイノルズの相似定理のようなことは言えなくなります。
この性質は、ジャンボ機などの航空機の機体の設計に応用されています。機体の性能を知るために、機体の縮尺模型による風洞実験が欠かせません。(いちいち本当の大きさの機体を作っていたら、まったく効率的でないですから。)機体のサイズが変わるとレイノルズ数も変わってしまいますが、風速を適当に調節してやれば、実際に飛行機が飛んでいるときのレイノルズ数と一致させることができます。この時、機体の回りの空気の流れは、本物の機体の回りの空気の流れと完全に一致します。そうすることで、実際に本物の機体を飛ばさずして、機体の性能を知ることができるのです。我々が安心して飛行機に乗れるのも、このレイノルズ数あってのことです。
興味深いことに、レイノルズ数は生物の体のつくりにも関係しているようです。興味のある人は、本川達雄著「ゾウの時間、ネズミの時間」(中公新書)を御覧になってみて下さい。
単位をどのように決めるかは、全くもって人間の所業であり、多分に歴史的、政治的背景がついて回ります。例えば、現在は長さの単位として、m が使われていますが、これはフランス革命後に国内の単位を統一した時に決められた単位で、地球の一周の長さを4万km とするように決められました。この1[m] の長さを決めるのにどれほど苦労したかは、有名な話であります。なぜこんな苦労をしてまで、単位を決めたのか?それは、地方によって単位がバラバラだったらどうなるか、を考えてみれば容易に想像できます。国全体が統一された単位を使えば、とても便利です。なぜなら単位を統一するためには、強力な権力を持つ国家が、その単位を使うように国民に強制しないといけないからです。事実、中央集権国家が多く成立した中国では、新しい王朝ができる度に、度量衡の統一が行われていますが、多くのポリスが発達したギリシャでは、ついに単位の統一はなされませんでした。それ以上に単位の統一が、国を一つの国家としてまとめあげる役割も果たします。
単位は物体の性質を数値化する時に必要なものです。物理学は、この数値化された量に注目する学問です。ですから、物理学では単位がとても重要なのでした。物体の性質を数値化するには、実際に物体の性質を「測る」ことをしなければいけません。例えば、物体の密度とか抵抗とか、あるいは物体の速さなどを実験によって「測る」ことができます。最近は物理の授業の中で物理実験を行うことが少なくなり、この「測る」ということが少なくなってきていると聞きます。しかし、物理に限らず自然科学の分野ではこの「測る」ということが、とてもとても大切なことなのです。このことをちょっとでもいいですから、心に留めておいてください。
しかし世の中には「測る」ということができない事もあります。例えば、音楽や絵画の価値などというものです。「測る」ことが仮にできたとすると、すべての音楽や絵画を数値化して一本の数直線上に並べることができます。しかし、音楽や芸術はそんな単純なものであるわけがありません。
「測る」ことができないものに対して、科学は何もいうことができません。そこが科学の限界であり、そして同時に音楽や芸術の面白いところです。しかし、時折大人たちは「何でも測る事ができるはずだ」という科学者の悪い癖をまねします。その代表例が「偏差値」です。何で大人たちが「偏差値」のようなもので子供を測りたがるかを知っていますか?そのほうが、大人たちにとって楽だからです。しかし、所詮人間を「測る」なんてことは不可能なはずです。どんな人も、もっともっと不思議で「測る」ことのできない何かを持っているはずです。
皆さんも友達を杓子定規で「測ったり」していませんか?
(補足)そういえば最近「作×の値打ち」という批評本がでていますね。この本は、なんと著作を100点満点で採点しています。すごい。だけど、これだって、あくまでこの批評者のなかのものさしですよね。彼が点を低くつけた中にも、面白いものはあります。(もちろん僕にとって。)あくまで参考に、ということでしょうね。